以斯帖統計顧問公司

由以斯帖統計顧問公司開設的『應用生物醫學統計研習營』已有多年歷史，藉由統計觀念的釐清以及統計軟體的實務操作，讓您頓時豁然開朗，閱讀SCI期刊論文也不再困難重重，擺脫學習統計學的包袱，重拾信心。而後期開設的『健保資料分析研習營』、『AI人工智慧研習營』也教育了許多有志於大數據分析的學員，使他們能獨立於各自的學術領域。2024年春季班正開放招生中，歡迎踴躍報名：

 各班課表

健保資料庫分析

2024: 07/13, 07/20(星期六) ：S1.基礎健保資料庫分析

2024: 08/03, 08/17, 08/24(星期六) ：S2.進階健保資料庫分析

有許多的軟體可以繪製地圖，例如ArcGIS、QGIS等地理信息系統軟體，簡稱GIS軟體(Geographic Information System)。但今天想利用SAS統計軟體介紹台灣地圖的繪製，程式參考SAS公司的部落格文章 ( 如何繪製地圖圖表 - SAS Taiwan )。

地理資訊中，包含經度，緯度，和海拔，以x、y、z坐標來標註。以及劃分疆界的地名，例如國名、縣市名、或鄉鎮市區名等。

我們可以從【政府資料開放平臺】的網站首頁，輸入【行政區界】，蒐尋台灣的地理資料，進入後，會有3種台灣的圖資可以下載，包括22縣市的圖資、368個鄉鎮市區的圖資，以及台北市12行政區的圖資。

下載檔案時，建議選擇SHP格式的圖資檔，SHP 是一種儲存地理圖資的檔案格式。

SHP格式的檔案是由數個檔案合成的，下載後，會收到一個.ZIP檔，解開後，裡面有幾個檔案，每個檔案會有不同的功用，但一定至少包含 3 個檔案： .shp (記錄地理圖資的點線面資訊)， .shx (地理圖資的索引)，.dbf (地理圖資的屬性資料)(參考政府資料開放平臺網站資訊)。

過去的文章曾介紹過ifn函數、dif函數、first.variable三種指令，這次，想以這三個指令，來介紹健保資料庫分析中的疾病定義。

在健保資料庫分析的各種疾病定義中，常聽到的一種定義方式為：任一年出現-二次某疾病診斷碼，並以此定義特定的疾病。

任一年二次以上的就醫記錄的概念，簡單來說，就是任意的兩筆資料間的天數差要小於一年，即365天。這是該定義最寬鬆的條件，因為一年內也可以有3筆或3筆以上的資料，但至少要2筆，且兩筆的天數差小於一年。如果第1筆與第2筆的就醫記錄超過365天，含365天，那麼.…我們要繼續往下找，看第2筆與第3筆間是否超過365天，並依此推算下去，直到所有就醫記錄全比對完。

1. ifn函數

首先，我們介紹ifn函數，n是numeric，數值的意思。這個函數包含4個參數，適用於數值型態的資料處理。而ifn，言下之意，就是針對數值型態的資料，在函數中寫條件句，並依不同條件執行資料處理的動作。

函數中的第一個參數是執行資料處理的條件，第二個參數是符合左列條件所要給予的正確賦值，第三個參數是不符合左列條件所要給予的錯誤賦值，最後一個是當資料為缺失值時所給予的賦值，這些值，都是可以自由定義的。

如以下範例所示：這個範例中的條件由餘數函數mod( )構成，函數中的x為被除數，2為除數，也就是x除以2的餘數為何？如果遇到資料為偶數，則為整除，餘數為0，正確賦值為1。遇到奇數，無法整除，餘數不為0，錯誤賦值為0。

 ifn(mod(x,2)=0,1,0);

透過這種方式，我們可以定義資料為偶數或奇數。

當您在分析健保資料時，一次要定義幾個診斷碼，甚至許多的疾病，有什麼SAS程式指令是有效率又好維護的呢？
這是 #以斯帖統計 的Youtube頻道新單元，這個單元是健保資料分析課程的Sophie老師為我們錄製影片！影片中介紹 #array指令 的操作，當您知道如何使用這指令，將更有效率地執行相似的重覆動作，例如將門診3組診斷碼定義為特定的疾病。

快進來看吧！希望能對您的資料分析有幫助。

/*--原始程式--*/

data aa;

本單元介紹如何自動儲存 SAS中的log及output輸出結果到指定檔案，如果我們利用SAS程式，將資料log及output輸出結果自動儲存到硬碟中指定的位置，可以寫以下程式，而詳細的說明請看Sophie老師的影片介紹。

範例程式

/*---建立虛擬的資料---/

data demo;
         do x=1 to 10;
        do y=1 to 12;

定量變數(Quantitative variable)包括連續變數(Continuous variable)與計數變數(Count variable)，前者包括身高、體重、體溫，後者包括懷孕次數、看診人數、每年空污人數。在這個單元中，不僅介紹資料的集中趨勢，也介紹資料的離散趨勢，還說明了盒形圖(box plot)與散布圖(scatter plot)的意義。 

以下是 #以斯帖統計 的Youtube頻道新單元，特別邀請交大統計博士－紅豆老師循序漸進地為我們介紹基礎統計的觀念，許博士不僅介紹觀念，還有清楚的統計軟體操作步驟喔！快來看看吧！

您一定聽過大數據(Big data)，但您認識大數據中變數值(Varaible)的資料型態嗎？統計中，資料的型態包括：「類別變數」(Categorical variable)，又稱「離散變數」(Discrete variable)，包括名義變數(Normal scale)以及次序變數(Ordinal scale)。而「連續變數」(Continuous variable)，且分為等距變數(Interval scale)及等比變數(Ratio scale)。名義變數的數字順序只是類別的代表名稱，沒有嚴重度的差異，例如性別、血型、種族，不可以做加、減、乘、除的運算。次序變數的數字順序有嚴重度的差異，例如滿意度與疼痛指數。

以下是 #以斯帖統計 的Youtube頻道新單元，特別邀請交大統計博士－紅豆老師循序漸進地為我們介紹基礎統計的觀念，許博士不僅介紹觀念，還有清楚的統計軟體操作步驟喔！快來看看吧！

在許多領域當中，我們常會需要處理按照時間先後順序所形成的序列資料，這類型的資料我們稱之為時間序列(time series)，像是金融領域裡預測股價的應用或是醫療領域裡心電圖的分析等，都是常見之時間序列，然而，要有效的分析時間序列一直都不是個簡單的事情。

一個時間序列通常可以被分解成四個部分，長期趨勢、季節變動、循環波動以及隨機波動。

長期趨勢指的是資料在一段時間內逐漸向上或向下的移動，例如人類近幾年來排放的二氧化碳數量逐年增加，其時間序列的趨勢很明顯就是往上的。

在來是季節變動，季節變動代表的是時間序列因某些季節因子而產生固定且週期性的波動，例如，每年12月聖誕節前夕，許多人都會為了慶祝此節日而產生更多的消費，而電商平台當月的銷售額也會因此增加，仔細觀察許多電商平台年銷售額之時間序列，往往就能看得出明顯的季節性。

循環波動指的是時間序列上所產生之不定期的波動，或是週期比較沒有那麼明確的波動，例如股票市場常每隔幾年會從多頭走向空頭趨勢，但我們卻無法精準且明確知道其多空頭的間隔要多久。

至於隨機波動就是所謂的不可預期之雜訊，它們通常沒有可以識別的形式，對於分析時間序列來說，是個相當頭疼的一部分。

然而，到底過去所發生的資料是否能預測未來呢?這個問題一直是分析時間序列最重要的事情之一，根據數學家發現，唯有時間序列呈現平穩狀態(*)，此序列才比較有可能被有效分析及預測。

那麼如果一個時間序列不是平穩的時間數列該怎麼辦呢?在數學上我們能使用所謂的移動平均發、d階差分等技巧，來讓時間序列傳換成平穩狀態，進而可以分析預測。

時間序列一直是一門博大精深的學問，也是許多專家學者正在努力嘗試突破的問題之一呢!

(*)所謂的平穩性指的是，一個時間序列的統計特性不因時間的變動而改變，即時間序列波型的平均、標準差、共變異數均不因時間改變而變動

撰文：李厚均老師 (Isaac)
出處：小李談數智（臉書粉絲頁）
插畫家：Yoshi Liao
近期課程：#深度學習理論 與 #TensorFlow之應用
課程訊息：https://www.estat.com.tw/product_1357510.html

在機器學習領域裡面，我們常常可以將問題分成兩種類型，一種是迴歸問題，而另一種則是分類問題，如何釐清我們所想要解決的問題是隸屬於那一類，是非常重要的一件事情，今天我們就來瞭解一下這兩種問題之間的差異吧！

當我們所要預測的目標為一個連續之數值的時候，我們便稱此類的問題為迴歸問題，而相對應的，當我們想要預測的目標為眾多類別當中的其中一種類別，那此問題則為分類問題。

舉個例子來說吧，假設我們想要藉由過往的金融資料去預測台積電明天的股價，由於股價是屬於一個連續的數值，因此像這樣一個問題就是屬於迴歸問題。然而，如果我們將問題改成預測明天台積電股價是否會漲還是跌，這樣一個問題則會變為分類問題。

在迴歸問題當中，我們期望能找到一條符合資料分佈的函數，這個函數可能不一定是線性函數那麼單純，很多時候可能是一個非常複雜的高維度函數！但如果我們真的能找到了一個不差的函數來擬合這些資料點，那麼我們便能藉由此函數來幫助我們預測未知資料點所對應的數值，這就是整個迴歸所想要解決的問題。

2010年歐盟EMA與歐洲ENCePP網路中心(European Network of Centers for Pharmacoepidemiology and Pharmacovigilance)共同發布「藥物流行病學方法學標準的指南」草案(Draft CUIDE ON Methodological Standards in Pharmacoepidemiology)，該指南是為了確保高品質的藥物流行病學研究，以加強藥品上市的安全性監測，以期維護民眾的健康，而今，ENCePP的指南仍是從事藥物流行病學研究及臨床流行病學研究的重要參考依據[1,2]，在該指南中提到了幾項重要的研究偏誤，是值得關注的。

利用健保資料庫分析作為藥物的安全性監測已行之多年，但不良的研究設計容易造成各種推論的偏誤（bias），其中一項重要的偏誤往往導致所觀察的藥物被宣稱對疾病有保護作用，或能降低不良反應，這種偏誤與觀察的時間有關，被稱為immortal time bias。

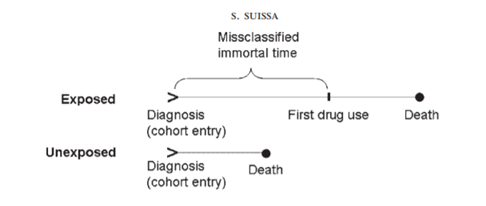
根據加拿大Suissa博士 2007年發表於Pharmacoepidemiology and drug safty[3]的文章所描述，許多文章都因immortal time bias而誇大了藥物的保護作用，若經由校正藥物的time-dependent definition後(後面會再解釋) ，研究結果就不再顯著，甚至結果是相反的。 並且immortal time愈長，造成的 bias就愈大 ，兩者成正比 。而immortal time bias是如何發生的呢?

Immortal time係指當病人被診斷為特定疾病至開始用藥的這段時間[2,3]， immortal time bias主要發生在Immortal time這段時間，一是將暴露組(用藥組)的person-time做出錯誤的歸類(misclassification)，二是將暴露組的Immortal time刪除。筆者試著以下面的兩張插圖(繪圖：S. Suissa PhD)做進一步的解釋：