在臨床實驗或介入型研究，經常需要對同一個受試個體(Subject)在不同的時間點觀察其反應，當觀察的時間點只有兩個時，可以用來分析的統計方法為paired t-test；如果觀察的個體數目太少，則會建議使用相依樣本的無母數檢定方法，如：Wilcoxon signed-rank test，若反應變項為類別型資料，且資料為相依樣本的情況下，其統計檢定方法為McNemar Test。
- 5月 18 週一 201516:41
重覆測量在生物醫學研究上的應用
在臨床實驗或介入型研究，經常需要對同一個受試個體(Subject)在不同的時間點觀察其反應，當觀察的時間點只有兩個時，可以用來分析的統計方法為paired t-test；如果觀察的個體數目太少，則會建議使用相依樣本的無母數檢定方法，如：Wilcoxon signed-rank test，若反應變項為類別型資料，且資料為相依樣本的情況下，其統計檢定方法為McNemar Test。
- 4月 28 週二 201516:34
『進階存活分析』在生物醫學研究上的應用
傳統的存活分析方法大多用於估計單一次事件(例如：死亡，得病等)的存活率，但是在臨床研究上，有些存活資料屬於復發事件(recurrent event)；例如，同一個體(subject)在追蹤時間(follow-up time)內發生多次某種症狀。以傳統的存活分析的觀點，可以僅看”第一次”復發事件的存活分析，但缺點是忽略了其他復發事件發生的訊息。所以，當資料型態是這種情形下，採用多次復發存活分析方法是較爲合適的。
一般的存活分析方法僅能用於資料之間爲獨立的情形下，然而，在臨床研究上，常收集到的資料是具有相關性的；例如，同一個體(subject)中的眼睛、腎臟等兩個以上的器官所收集到的存活資料。此外，同一家庭內的兩個不同個體的存活資料，亦可視爲此種資料型態。此種資料因爲具有配對的特性，所以在分析上較爲複雜，所採用的方法為配對存活分析(Matched Survival)。
在醫學研究中最常見的資料型態為右設限(right censored)資料，此類個案僅能記錄到從進入研究到研究截止的時間，在研究時間中止前，某些個案尚未發生感興趣的事件，所記錄的時間非真正發生事件的時間，造成資料不完整的情形。另一種常見的不完整情形爲左截切(left truncation)資料，左截切分析中，究者感興趣的是個案的存活年齡，例如65歲以後入住於老人安養院後能存活到幾歲。如果個案在研究開始前即死亡，則完全無法被觀察到，有別於右設限，左截切僅能觀察到部份的個案資料。在這種情形下，典型的Kaplan-Meier estimate是無法使用的。
另外。在醫學研究的實務應用中，可能存在有二種以上的不同事件，而感興趣的事件為其中一種。在這種情形下，出現某種事件可能會掩蓋了其它事件發生的可能性，此即為競爭風險(Competing Risks)。例如，針對白血病骨髓移植病患的研究，可能發生的事件有二種。白血病復發(relapse)以及移植失敗所造成的死亡(death)。如果我們要探討的是骨髓移植的復發率，移植失敗所造成的死亡(death)即為復發(relapse)的競爭風險事件(competing risk event)。所採用的方法為以累積發生函數(cumulative incidence function; CIF)來呈現特定事件在不同時間點發生的可能性。
- 1月 22 週四 201510:20
主成份迴歸
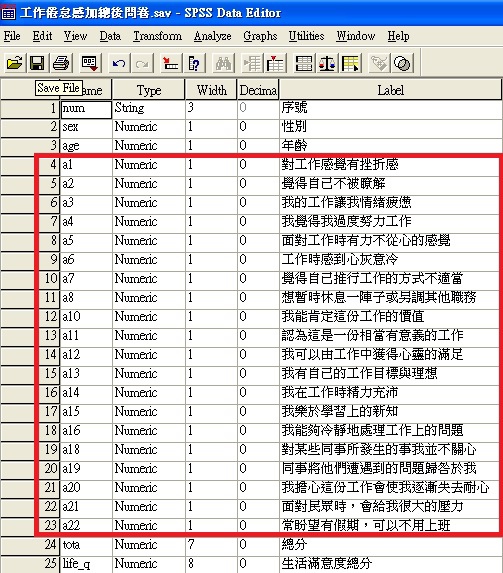當解釋變項間存在共線性問題，但又無法直接以剔除變項的方式進行多元回歸分析，此時可採用主成份回歸分析來減輕解釋變數間的多重共線性。以下以工作倦怠感預測生活滿意度為例，解釋變數包含年齡、性別及工作倦怠感量表上的20個測量題，如下的資料結構所示，但有幾組題目間存在著相當高的相關性，若同時放入回歸模式中會因共線性的關係影響模式的估計，如下表的相關係數表所示，第1-8題的相關性很高，第10-15題的相關性很高，同時第20-22題與第16-18題之間的相關性很高。因此可考慮將量表以主成份分析萃取出幾個成份(component)，使相關性很高的題目組成一個成份，而每一個成份間的相關性是最低的，並將每一個成份重新命名，且計算每一成份新的分數(score)，再進行多元邏輯斯回歸，如此即可解決多重共線性的問題，此法即主成份回歸分析法。在因素分析時，要用正交(或直交)轉軸法找出特定的成份，並為各成份命名，但命名的合理性是很容易受到爭議的。
- 1月 09 週五 201516:42
何謂次數分配(Frequency distribution)？讓一群舞者跳給您看！
通常我們收回集的資料乍看之下是很混亂，且讓人頭疼的。因此我們需要能從中找出資料的特性。由以下的舞蹈可以看到如何從混亂中衍生出規則，請注意！一開始，舞者的位置是雜亂的，動作有快亦有慢。之後，我們可以看到舞者頋依據他們的速度重新排列位置，跳得慢的站在左邊，快的在右邊，其餘的在中間。他們產生了次數分佈，水平方向呈現的是速度，垂直方向呈現不同速度的個數，這樣的分佈近似常態分佈(normal distribution)或稱高斯分佈(Gaussian distribution)。特別要留意的是，很少的舞者站在特別快或特別慢的位置，大部份的舞者屬於中等速度且站在中間，這樣的資料分佈特徵為鐘形曲線(bell-shaped curve)。
- 12月 10 週三 201405:51
直接標準化死亡率(Direct Standardize Mortality Rate)
為了計算不同族群間、或不同時期的率差或率比，必需以標準人口結構調整死亡率才能進一步比較，否則因不同族群、或不同時期的人口結構不同，則會影響比較結果。標準人口通常是一組大而人口結構穩定的族群，例如全國人口，若要進行國際間的比較，將以2000年世界標準人口進行標準化(不分性別、每5歲一個年齡組距)。
- 11月 10 週一 201417:52
分層隨機抽樣法(Stratified Random sampling)
- 10月 03 週五 201416:23
抽樣與標準誤(Sampling and Standard Error)
當我們想瞭解一個大群體(或稱母群體；a population)的資料特性，但礙於人力、經費與時間等現實因素，我們無法收集到母群體完整的資訊，於是會藉由抽取一部份的樣本以代表母群體，並利用抽樣結果描述母群體，而每次的抽樣結果與母裙體間的偏差即為標準誤(Standard Error)。它與標準差(Standard Deviation; SD)雖然只有一字之差，但意義完全不同。標準差為每個樣本與樣本平均值的偏差(Deviation)，用來描述一組樣本的分散情形。
- 9月 17 週三 201418:32
淺談Moses 極端反應檢定方法(Moses extreme reactions test)
在許多臨床試驗中，由於針對某些疾病個案的收集不易(或是phase II trial ,僅收集較少的個案)，所以造成後續可用來進行統計分析的樣本數不大，此時常見的分析方法爲無母數方法(non-parametric method)。針對數值型的反應變項(response)，如欲比較實驗組和控制組間，反應值是否有差異，Mann-Whitney U test爲最常用的分析方法。然而，當反應值的分佈狀況並非聚集於中央，而是群集於兩端時，Mann-Whitney U並無法適切地呈現比較的結果。例如治療焦慮(anxiety)的用藥，對某些人來說有可能降低焦慮的症狀，但對某些人來反而會更加嚴重，此時焦慮反應程度便是分佈於兩端。
上述的例子中，使用Moses 極端反應檢定方法是更爲恰當的選擇；也就是說，比較的是兩組資料的散佈狀態(dispersion)是否相似。不同於Mann-Whitney U test, Moses 極端反應檢定的虚無假設爲H0: 兩組的極端值是相近的。所以，當研究者有合理的證據(文獻佐證)認爲反應值的資料並非集中於中央，而是偏斜(skewed)或群集於兩端時，Moses 極端反應檢定方法更加適當。在統計軟體的運用方面，SPSS中無母數檢定模組中即有此檢定方法；另外，SAS以及R也可以進行Moses 極端反應檢定，此檢定方法幾乎可見於大部份的統計軟體。
Reference:
Moses, L. W., "Non-Parametric Statistics for Psychological Research," Psychol. Bull., 1952, 49, 122-143.
- 9月 16 週二 201411:11
有序型資料的比較：參照特定分佈單位分析(Ridit analysis)
在許多醫學研究中，所收集到反應變數的資料爲有序型態(ordinal data)；例如評估某種疾病嚴重度, 0, 1, 2, 3, 4此即爲典型的有序資料----也就是說，數字本身除了區分嚴重度的不同類別外，數字的大小還具有程度上的差異。針對此種資料，當成連續型資料來分析並不合適，而使用類別型資料常用的卡方檢定則無法兼顧到有序資料的所有特性，所以常見的分析方式爲無母數的Kruskal-Wallis H test。而Bross在1958年提出了另一個方式：計算Ridit score來分析。其想法爲先找一較大的資料爲標準母體，計算出ridit score(爲0~1之間的數字，代表位於某一等級的累積機率)，再將算出的ridit score取代原先的各組的有序資料來進行傳統的連續型資料分析；換句話說，將原先的有序資料轉換爲連續資料，再進行像各組平均值比較(t test, ANOVA)等方法。
- 5月 23 週五 201419:05
您知道何謂Correlation(相關)？讓一群舞者跳給您看！
原來統計觀念的傳達方式可以這麼多元，今天要介紹的影片是由英國心理學會 (British Psychological Society; BPS) 募集資金製作的，希望透過舞蹈的趣味讓更多心理學系學生對統計觀念有更深刻的印象，是否覺得英國人很有創意呢？